asa: angle, side, angle
Given
\(\angle C\), \(a\), \(\angle B\) - two angles and the included side
Analysis
We can locate the first vertex of the triangle, \(C\) or \(B\), by constructing one of the given angles, \(\angle C\) or \(\angle B\) correspondingly. Let us assume that we have picked the given angle \(C\), constructed it and located the vertex \(C\). We can now use this vertex as a center of a circle constructed with the given side \(a\) as its radius. The intersection of this circle with one of the sides of the constructed angle \(C\) will locate the second vertex of the triangle, \(B\).
To locate the third vertex of the triangle we need to construct the remaining given angle, \(\angle B\) in this case, with the point \(B\) as its vertex. Both given angles, \(\angle C\) and \(\angle B\), share one side with each other - the side \(a\). Two other, not shared, sides intersect at the third vertex, \(A\).
Construction Outline
Construct the given angle \(C\) with the vertex at an arbitrary point \(C\). Cut the given side \(a\) on one of the sides of the angle \(C\) at the vertexes \(C\) and \(B\). Construct the given angle \(B\) at the vertex \(B\). The intersection of the not shared sides of the angles \(C\) and \(B\) locates \(A\)
Sample Construction
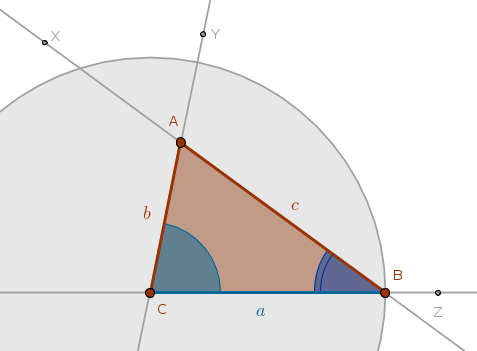$$C, Z$$
$$Ln(C, Z)$$
$$Y \colon \quad \angle YCZ = \angle C$$
$$Ln(C, Y)$$
$$Cir(C, a)$$
$$Cir(C, a) \; \cap \; Ln(C, Z) = B \colon \quad CB = a$$
$$X \colon \quad \angle XBC = \angle B$$
$$Ln(B, X)$$
$$Ln(B, X) \; \cap \; Ln(C, Y) = A$$
$$\triangle ABC$$
\(\blacksquare\)