sss: side, side, side
Given
\(a\), \(b\), \(c\) - all three sides of a triangle with a stipulation that the sum of any two sides is greater than the remaining one:
$$a + b > c$$ $$a + c > b$$ $$c + b > a$$This is an all time classic - Euclid carries out this construction in B1P22 which itself is a generalization of B1P1 - an equilateral triangle construction.
Analysis
We start with an observation that three vertexes are needed to construct a triangle. In this particular case we can locate two vertexes by choosing an arbitrary given side and cutting its length on an arbitrary line. We can then use these vertexes as centers of circles built with the remaining sides as their radii to locate the third vertex of the triangle. These circles will intersect at two points but one is enough.
For this construction to work two postulates missing from Euclid's "Elements" are needed. The first one should state:
if the distance between the centers of two circles is less than the sum and greater than the difference of their radii then these two circles intersect
The second postulate should state:
two straight lines intersect at one point at the most
The first postulate gives the intersecting circles the right to exist and spells out the conditions under which this event can occur. In the construction below this postulate gives the right for the point \(A\) (and its counterpart) to exist. The second postulate is needed to ensure that the straight lines on which the radii of the circle lie intersect at exactly point \(A\) and nowhere else.
Construction Outline
Construct the given side \(a\) at the vertexes \(C\) and \(B\). Construct a \(Cir(C, b)\) and a \(Cir(B, c)\). The intersection of these two circles locates \(A\)
Sample Construction
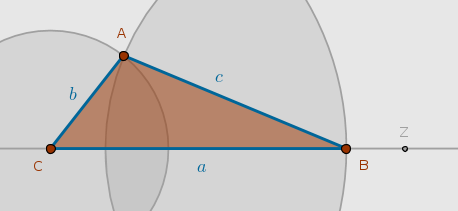$$C, Z$$
$$Ln(C, Z)$$
$$Cir(C, a)$$
$$Cir(C, a) \; \cap \; Ln(C, Z) = B \colon \quad CB = a$$
$$Cir(C, b)$$
$$Cir(B, c)$$
$$Cir(C, b) \; \cap \; Cir(B, c) = A \colon \quad CA = b, BA = c$$
$$Ln(A, C)$$
$$Ln(A, B)$$
$$\triangle ABC$$
\(\blacksquare\)